PSpice(評価版)でNo−168をシミュレートする
その2
感涙(;_ ;)
K式御用達半導体素子の定義ファイルがやってきた。
ありがたきかな。m(__)m
こうなれば、これまで代替素子に外部Cをかますなどしてやってみたシミュレーション、これでやり直してみなくては・・・(^^)
と、思って、早速No−168CDラインアンプの回路を組んでみたのだった。
いかなることになりますか・・・(^^;
終段に燦然と輝く2SC959!!
本物の方は殆ど入手不可能となりつつあるこんないにしえのトランジスタのSPiceモデルなんて、ほんとにあっていいのだろうか?
などと考えてもしょうがない。
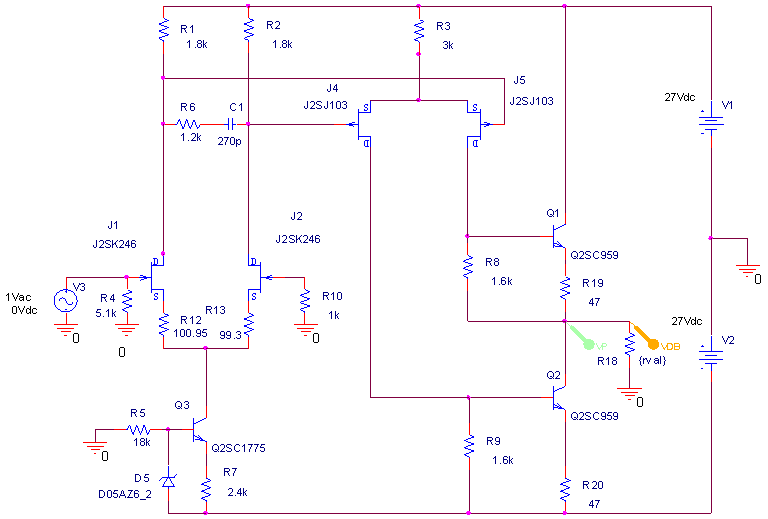
ので、早速負荷1kΩ、2kΩ、4kΩ、8kΩ、16kΩ、32kΩ、64kΩのパラメトリック解析でオープンゲインの周波数・位相特性を観る。
2段目差動アンプの共通ソース抵抗値が3kΩになっている。のは、このモデルに用いた素子のばらつきで終段のアイドリング電流を適正値にするために必要だったから。この辺は現実の場合と同様で、まるで本当に作っているかの如くだ。
が、そうでなくてはシミュレーターとは言えない。
アンプ出力の負荷が1kΩでのオープンゲインは低域で44dB、fc(−3dBポイント)は約90kHz、負荷64kΩでは69.5dB、fc≒12kHz。
No−168のK先生の実測データでは、負荷1K時40dB、fc≒90kHz、負荷51kΩ時68dB、fc≒7kHzであるから、このモデルはややゲインが大きく、かつ、高域特性も多少良い結果が出る、ということになる。
その要因は何か?は、それ以上の比較データがないので分からない。のだが、多分2SC959のモデリングの問題だろう。何故ならこのアンプのゲインの殆どは2SC959によるものであるなど、このアンプの主役は2SC959だからだ。
が、なかなか良さ気な結果だ。(^^)
詳しいことは知らないが、NFBアンプのポイントは、K式での一般である初段差動アンプ反転入力をNFB入力とする場合はNFB信号の位相が入力信号の位相と同相でなければならないということである。これが逆相(=180°の位相回転)になってしまうとNFBがPFB(=正帰還)になってしまい、アンプは発振状態に陥る。
ので、NFB信号の位相が回転してPFBにならないようにしなければならないのだが、オーバーオールNFB信号は通常アンプ出力からフィードバックされるので、回路内部の時定数により残念ながら位相回転は避けられないのである。この位相回転が180°に達してしまえばもうアウトだが、とりあえず位相回転が120°以上回転する前にアンプのループゲインが1倍(0dB)以下になるように設定すれば、信号を初段に戻してNFBを掛けても大概は安定に動作する。ということらしい。
ループゲインが1倍(0dB)になるポイントとは、単純にはオープンゲインとクローズドゲインがイコールであるポイントということだ。No−168の場合ボリュームMin.の際は帰還率β=1である。この場合上のグラフのとおり負荷1kΩのオープンゲインは低域で44dBであり、クローズドゲイン設定は0dBである。だからループゲインは低域で44−0=44dBである。が、10kHz付近からオープンゲインは徐々に低下し、ということはループゲインも徐々に低下し、10MHzでオープンゲインも0dB、クローズドゲインも0dBとなるので、そのポイントでループゲインが0−0=0dB=1倍ということになる。
このポイントより低い周波数ではループゲインが1倍以上あるから、帰還電圧の位相が回転して正帰還になってしまえば増幅機能により拡大再生産が続くので発振してしまうが、このポイントより高い周波数ではループゲインが1倍未満であるためにそもそも拡大再生産には陥ることがないので、位相が180°回転して正帰還状態になっていてももはや発振には至らないのである。だから、このループゲインが1倍になったポイント、ここでは10MHzだが、そのポイントにおいて位相回転が120°以内に収まっていれば、それより高域で位相がそれ以上回っても問題なく、また、ループゲインが1倍以上あるそれより低い周波数での位相回転も通常はそのポイントより少ない(すなわち120°以内)ので、アンプは決して発振することなく安定に動作する、ということなのである。
この事例では高域でループゲインが0dB=オープンゲインが0dBに沈むポイントは負荷に拠らず10MHzであるが、その点での位相回転は−130°弱である。完全に−120°以内ではないが−180°に対しての位相余裕はまだあるので、多分この状態でゲイン0dBまで絞る(=44dBのNFBを掛ける)ゲインコントロールアンプとして安定動作が可能であろう、ということが分かる。
なお、ループゲインが1倍になったポイントにおいて位相回転が−120°以内に収まっていれば、ループゲインが1倍以上あるそれより低い周波数での位相回転も通常はそのポイントより少ない、と言っても、この場合のようにステップ型の位相補正を使用した場合は必ずしもそうならないので、この点注意が必要だ。この場合は300kHz付近での位相回転がそれである。が、ここではそれも−120°以内に収まっているので大丈夫だろう。
で、なかなか良さ気な結果だ。(^^) というわけである。
現実に近いシミュレーション結果なのではなかろうか。と思える。
初段の位相補正素子を外して同様にシミュレートして比較すると、初段ステップ型位相補正の意味と効能が分かる。
ステップ位相補正の低域側周波数は、159/((1.8+1.8)・0.00027)≒164kHzである。
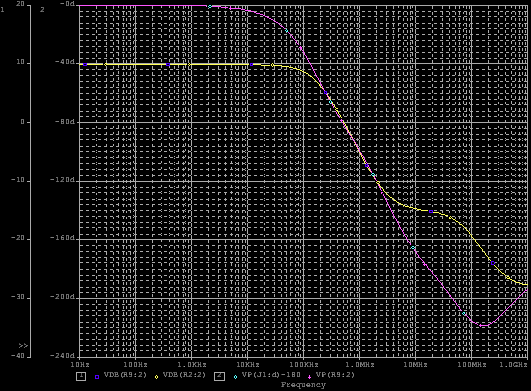
下のグラフから、スッテプ位相補正をしていない状態では1MHz弱まではワンポールであり、結果位相は−90°までしか回転していないということが分かるが、上の場合のように初段にステップ位相補正を入れるとその164kHzの低域側ポールにより位相回転が早まってしまい、300kHzで位相回転が−120°まで達っする。という違いが良く分かる。
位相回転が早まってしまうというのはわざわざ危険な方向に舵を切るということである。なのにそれでもステップ位相補正を使うのは何故か。
虎穴に入らずんば虎児を得ず。それは高域側を見ると分かる。
初段ステップ位相補正のない状態では、高域でオープンゲインが0dBに沈むポイントは20MHz弱と伸びる。すなわちそこがループゲインの0dBポイントである。のだが、そのポイントでの位相回転は−180°に達してしまうのである。したがってこの状態のままNFBを掛けるとNFB=負帰還が負帰還でなく正帰還になってしまうのでアンプは発振してしまうことになる。
そこでステップ位相補正なのだが、その高域側周波数は、159/(1.2・0.00027)≒491kHzである。
ステップ位相補正は、低域側周波数で利得は−6dB/octの減衰カーブを形成し位相も−90°へ向けて回転するという通常のポールと同様の効果を発揮するのだが、この場合低域側周波数と高域側周波数に1オクターブの間隔がとられていないから、その利得減衰は落ちきらないうちに高域側周波数ではもう平坦に戻り、その地点まで回転していた位相もその周波数からは0°に向けて逆回転するという効果を発揮するのだ。
このステップ高域側効果が、下のグラフの他のポールによる利得減衰や位相回転の効果に加算される訳だが、結果、上下のグラフと比較してみると分かるように、ステップ位相補正をした上の場合、利得減衰の方は全体としては減衰周波数が低域側にシフトするが、500kHz付近から利得の減衰カーブが微妙に緩やかになっているという結果になっているし、位相の方は、低域側で位相回転を早めたものが300kHzから400kHzを底として逆回転に転じ、2MHzから3MHzでの−105°を頂上として再び回転するというという状況になる。
ここで3MHz以降再び−方向への回転を早めるのは、4MHz以降に第2ポール以降のポールが存在するからである。90kHz付近の第1ポール以外にポールが存在しなければ、高域ではステップ位相補正の位相回転効果は0°となるので、その結果位相回転は−90°まで戻るはずなのだが、この場合は第2ポール以降のポールがさらに高域に存在しているため、その位相回転効果で−90°まで戻らないうちに再回転を余儀なくされている訳だ。が、最終的に3MHz以降にもステップ高域側の位相戻し効果が残るために10MHzでも位相回転が−130°弱となって、結果、絶妙に必要な位相余裕が確保される、ということになる。
実に上手い塩梅だ。が、塩加減を間違うとどうにもならない。といった感じなのがステップ位相補正。(^^;
さて・・・、基本的なところをシミュレーションで確かめてみるのもいいわなぁ(^^;
という訳で初段2SK246のVgs−Id特性を観る。
電流プローブをドレインに接続し、DCスイープモードでV2を−3Vから0Vまでスイープする。Vdsは10Vだ。
即座に右のグラフのとおりVgs−Id特性(Vds=10V)が表示される。
これでこの2SK246が、Vgsのカットオフ電圧−2.5V、Idss=5.8mA(Vds=10V)のGRランクの2SK246であることが分かる。No−168の初段の動作設定は1mA強であるが、このモデルの場合Vgs=−1.55Vでその程度のIdになる訳だ。
この程度の測定でも、自分で実際に測定しようとすると機器も手間もそれなりにかかる。それを一瞬でやってくれるシミュレーターは全くありがたいものだ。が、その結果が正しいものであるかどうかについてははっきり言って分からないのである。勿論世界的に活用される実績あるソフトウェアであるから正しいという蓋然性は高いであろう。が、結果に疑いの目も向けて、何故シミュレーターがそのような結果を出すのか、その辺を自らも考えながらシミュレーション結果を判断しないと、時に大きな間違いを起こす。
な〜んて偉そうなことを言って、自ら考えてみても間違うやつ > (^^;
さらにV1も5V、20V、35V、50Vとスイープする。
すると、右のようにVds=5V、20V、35V、50VにおけるVgs−Id特性が一挙に表示される。勿論下からVds=5V、20V、35V、50Vの場合だ。同じVgsならVdsが高いほどIdが多くなることが分かる。が、その量は微量だ。出力インピーダンス(出力抵抗)が大きいためである。
Vgs−Id特性を表す曲線の傾きが順方向伝達アドミッタンス=|Yfs|ということになる。要するにゲートソース間電圧の変化がどれだけのIdの変化に変換されるのかということである。1Vが1Aに変換される場合1Sとなる。こういう小信号用FETでは1V入力で数mA程度変化するだけなのが通例で、すなわちその|Yfs|は大概数mSから大きくても数10mS程度だ。
これと同じ内容のことを真空管時代には相互コンダクタンス=gmと言ったらしい。単位はモーでΩを逆さまにした記号で表した。
|Yfs|は打鍵が面倒、モーの記号はコンピューターで出てこない。なので、gm=○mSなどど混乱した使い方をしている。> (^^;
結局、このグラフから、素子自体のgmはもともと一定ではなく、Vgs値により、Id値により、また、Vds値によっても違ってくるということが分かる訳だ。
どの程度の出力インピーダンス(出力抵抗)であるかを観るため、Vgsを−2.4Vから0Vまで0.4Vごとに設定した場合のId−Vds特性を測定してみる。
グラフ一番上がVgs=0Vの場合で、以下0.4V毎にVgs=−0.4V、−0.8V、・・・で一番下がVgs=−2.4Vの場合である。
グラフの傾きは出力インピーダンス(出力抵抗)を表している。このグラフでは目盛が荒いため正確に計算できないが、数百kΩといったところだろうか。やはりIdは少ない方が出力インピーダンス(出力抵抗)は高いことが分かる。
ついでだが、この特性はいわゆるエキスパンダー特性だ。まぁFETは二乗特性なのでエキスパンダー特性にならないとおかしいのだが(^^;
直流バイアスを−1.55Vに設定し、1Vacを入力に加えて電流ブローブでドレイン出力電流を測定すると、電流プローブは交流出力電流値を表示する。gm=|Yfs|とは、1V入力が何Aの出力電流に変換されるかを表すものであるから、ここで1Vacを入力すれば、電流プローブ出力値がそのままgm=|Yfs|値である。すなわち、これでNo−168の初段の動作電流値であるId≒1mAにおける2SK246のgmが測定できるのだ。
電流プローブは2mAを表示している。したがって2SK246のgmはgm=2mS(Id≒1mA、Vds=10V)である。
スペースの無駄なので表示しないが、実は縦軸を拡大するともっと正確に分かって、gm=1.9939mS(Id≒1mA、Vds=10V)である。
そこで、回路設定にあわせて、Vds=27Vとして、負荷抵抗R1も挿入してgmを測定してみる。
パラメトリック解析でR1=0Ω、1.8kΩの場合である。
結果、R1=0Ωの場合、gm=2.0705mS、R=1.8kΩの場合、gm=2.0508mSであることが分かる。
負荷に1.8kΩが入るとgmが0.02mS小さくなっている。何故か?
それは2SK246の出力インピーダンスのためである。
この場合、2SK246自体の素子gmが2.0705mSであり、回路GMが2.0508mSなのである。
2SK246の出力インピーダンスをRoとすると、
GM・R1=gm×(Ro×R1)/(Ro+R1)である。
したがって、この関係から2SK246の出力インピーダンスが計算できる。
式を変形すると
Ro=Gm*R1/(gm−GM)であるから、
Ro=2.0508×1.8/(2.0705−2.0508)≒187kΩ である。
念のため、2SK246の出力インピーダンスをId−Vds特性(Vgs=−1.55V)からも計算してみる。と、Vds25V付近ではVds=15VでId=1.162mA、Vds=35VでId=1.22mA、すなわちVdsの20V増加でIdが0.058mA増加するのでRo=20/0.058≒345kΩである。
合わない。
Ro≒187kΩとRo≒345kΩ、では誤差の範囲とは言えない。どちらかが間違っている。
とすれば、こちらだろう。負荷に1.8kΩが入った場合そのVdsはその電圧降下で25V程度になる。であれば無負荷時のgmもVds=25Vで測る必要がある。
結果、gm=2.06158mS(Vds=25V)とでた。
Ro=Gm*R1/(gm−GM)を計算し直すと、
Ro=2.0508×1.8/(2.06158−2.0508)≒342kΩ である。
これなら読みとり誤差の範囲だ。
初段にはソース抵抗も入る。200Ωの半固定抵抗だが、片側には大体100Ωが入ったことになる。これは信号入力に対しVgsとシリーズになる。だから電流帰還によるNFBが働く。
これの影響は、まずgmの低下。
gm≒1.69mS
たったの100Ωだが、gmが2割も減ってしまう。
出力インピーダンスは大きくなる。
Vds=15VでId=1.137mA、Vds=35VでId=1.18mAだるから、Vds20V増でId0.043mA増。
20/0.043≒465であるから
Ro≒465kΩ、と出力インピーダンスは4割増しである。
gmの直線性は良くなる。のは、Vgs−Id特性からも分かる。
ただし、もともとの素子gmが小さいのでソース抵抗100ΩによるNFB効果も小さく、直線性の改善効果はそれほど顕著ではない。
gmが小さくなったため、傾きが全体的に緩やかになっている、といった風情だ。
gmが小さくなれば、当然電圧ゲインも小さくなる。電圧マグニチュードプローブと電圧位相プローブを取り付けて観測する。
まずはソース抵抗がない場合。
G=2.06158mS×1.8kΩ=3.71倍=11.39dB になるはずだが、右のとおりそうなっている。
ソース抵抗でgmが小さくなった分電圧ゲインも小さくなるはず。
この場合のgm≒1.69mSであったから、G=1.69×1.8=3.04倍≒9.65dBとなるはずなのだが、・・・そうなっている。
ソース抵抗があってもなくてもfc等の増幅帯域特性や位相特性には変化が見られない。のは、理想電圧源(出力インピーダンス=0Ω)でドライブしているからであろう。すなわちこの特性は2SK246の天賦の特性である。ということになる。
実際の初段の周波数特性は前に繋がる機器の出力インピーダンスによって悪化してしまう。
例えば10kΩとしてシミュレートしてみる。
fc=1.7MHz程度であろうか。
これは2SK246のCrss(出力容量)によるものであろう。
2SK246のCrssは規格上2.5pFであるが、ドレイン側に電圧ゲインが3.04倍あるのでミラー効果によりその容量は2.5×(1+3.04)=10.1pFに拡大される。
したがって、2SK246の入り口にfc=159/(10*0.0000101)≒1.57MHzのポールが発生する。
多少の違いは、読みとり誤差、または、規格上のCrss=2.5pFはVds=10V時でVdsがより高圧になるほどにその値が減少することをシミュレーターの方は正確に計算していること、によるものと思われる。
初段差動アンプである。
初段差動アンプはきちんと対称動作をするのであろうか。が、テーマ。
左右それぞれのgmを観ると分かる。
初段は、差動の片側にしか入力がないので、入力信号がJ1とJ2に1/2づつ分配されるから、結果gmはそれぞれに単独の場合のgm≒1.69mSの半分、1.69/2=0.845mSになるはずだ。
差動の左側はそうなっている。が、差動の右側はそれよりやや低く0.805mS程度だ。
差動アンプなのに左右の対称性がイマイチではないか。特に10MHz以上の高域ではその乖離は大きい。
何故だ? って、実はわざと共通ソースを13kΩの単なる抵抗にしているのがみそなのだが・・・(^^;
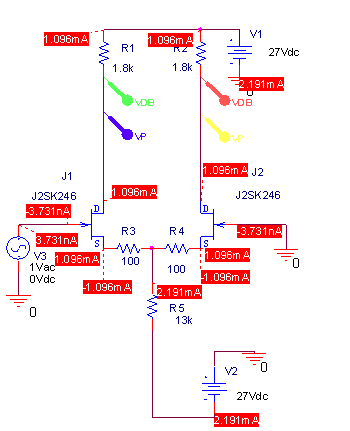
右のとおり、この時左右の2SK246に流れている動作電流は全く一致している。
にもかかわらず、その電圧ゲインと位相特性は下のグラフのようになってしまう。
電圧ゲインはやはり差動の右側が0.5dB弱左側より小さい。
位相特性は逆に右側の方が高域でやや良い結果になる。
何故だろう?
まぁこれは、某氏が以前指摘されたとおり、不平衡入力差動増幅器の非対称性であろう。この場合、右側の2SK246のゲートは接地されており、ベース接地動作をしているに違いないのに対し、左側の2SK246の方は典型的ではないがエミッタ接地動作をしている。ということらしいので、故に多少の違いが生じる。違うか?(^^;
この場合でも、次のように差動右側に180°回転した1Vac入力を加え、差動アンプを平衡入力状態にすれば、左右ともにgm=1.65mSで高域までピッタリと一致した特性になる。
ちなみにこれはK式DCアンプで2段目差動アンプに使われている状態である。もちろんNo−168でもそうだ。
入力が平衡状態で加わるのであれば差動アンプの共通ソース(エミッタ)側は高インピーダンスの定電流回路でなくとも良いのだ。とりあえずは・・・(^^;
では初段差動アンプはどうか。今度は定電流回路を使用する。ここに13kΩの抵抗を起用した上の場合と比較すると、何故ここに定電流回路を起用するのか、その理由が分かる。
不平衡入力差動増幅器状態であるのに、右のとおり左右のgmは0.835mSでピッタリ一致している。
なるほど。差動アンプの要(カナメ)は良く言われるとおり定電流回路にあるのだ。定電流回路で共通ソース(エミッタ)回路を構成すると、不平衡入力差動増幅器状態であっても差動アンプは平衡入力差動増幅器状態に近づくのだ。要するに理想的な差動増幅器に近づくわけだ。
初段の定電流回路をいじると音が変わるとおっしゃる耳の敏感な方も多いが、この辺にもその理由があるのだろう。
しかしながら、残念なことに超高域の特性差はこれでも改善されない。
これはやはり平衡入力状態にしないと改善しないようだ。まぁ、これだけ高域まで特性が一致するなら十分であるとも思えるが・・・(^^;
差動アンプの共通ソース(エミッタ)側を定電流回路にすると、左右の差動アンプの特性の一致が図られるのは何故か?は、残念ながら良く分からない。
また、特性の一致が図られると言ってもMHz以上の周波数領域においては対称性は破れる。この点においてやはり不平衡入力差動アンプには限界がある。
結果、初段における電圧ゲイン及び位相特性は下のグラフとなった。
初段の電圧利得は3.4dB、fc=20〜30MHz。
最終的に10MHzでループゲインが0dBに沈むことを勘案すると、十分な対称性だと思える。
2段目差動アンプである。
こちらは初段の差動出力によって平衡ドライブされる。
平衡ドライブされると、共通ソース抵抗が3kΩと低くても左右の差動アンプの特性は超高域までピタッと一致する。
gm=1.955mSである。
2SJ103のVgd−Id特性。
この2SJ103はG・Sカットオフ電圧2V、Idss=−5.6mA(Vds=10V)のGRランクの2SJ103であることが分かる。
2SK246もIdss=5.8mA(Vds=10V)であった。2SJ103と2SK246はコンプリ指定であるためIdssが等しいモデルとなっているのかもしれない。が、そのG・Sカットオフ電圧は−2.5Vだ。したがってIdssが等しくてもgmはどのポイントでも一致しない。まぁ、コンプリといってもそんなものである。
No−168での動作電流設定は0.5〜0.6mA程度である。
そこでVgsを1.5Vに設定し、V1を0Vから50VまでスイープしてIdの変化から2SJ103の出力インピーダンスを計測する。
Vds30Vの増加でId0.01mAの増加である。したがって2SJ103の出力インピーダンスは、30/0.01=3MΩだ。
No−168製作記で実測したときはこれが8MΩとなった。が、あれはテスターの狭い目盛のところで目視で測定したので測定誤差が大きい。
はたしてどちらが正しいのか?ということになれば、測定環境を考えるとこの3MΩを採用することになる。(^^;
2段目は、初段の負荷抵抗1.8kΩがドライブインピーダンスであるので、1.8kΩを取り付けて電圧利得とその位相特性を観る。
電圧ゲイン10dB=3.17倍、fc≒6MHzである。
gm=1.955mSであったから、G=1.995×1.6=3.192倍となるはず。ゲインは計算どおりである。
ではfcはどうか。2SJ103の規格ではCrss=3.6pFである。したがって計算上fc=159/(1.8×(0.0000036×(1+3.17)) である。これを計算するとfc=5.88MHz。ピッタリだ。が、これはちょっと出来過ぎ。というものだ。
この平衡入力差動増幅器状態の2段目差動アンプに、平衡を欠く要素を盛り込んだ場合どうなるのか。を考える。
先ずは、位相補正のためにドレイン−ゲート間に入れるコンデンサー。
両側に同じく入れれば勿論対称性は崩れない。
fc=159/(1.8×(0.0001036×(1+3.17))=204.5kHz とピッタリのようだ。
では、差動の片側だけに位相補正のCが入った場合はどうか。
差動の効果は確かにある。
が、限界も表れている。
C1による右側のfc低下作用は、差動動作の効果により左側にも伝達され、左側にはCを入れていないにもかかわらず左側もfcが低下する。
ところが、その差動動作の効果には限界があって、周波数がfcポイントより高くなるほどに左側はもとの状態に戻ってしまうようだ。
もしや共通ソース抵抗を電流源(=理想的定電流回路)に置き換えればこの非対称も改善されるのではなかろうか。
が、結果は右のとおりで、僅かに改善されるのだが、やはり根本的には改善されないようだ。
次は、負荷の非対称要素。
2段目差動アンプの右側だけに負荷抵抗32kΩを入れ、左側は負荷抵抗を入れず−電源に直結する。
信号を片側からだけ取り出す場合、こういうふうに差動アンプのもう一方を電源に直結する回路は一般には普通に使われているようだ。
が、K先生はいにしえに、こういう動作のさせ方は差動アンプのバランスを崩し妥当でないと仰っていたのである。
ではあるのだが、現代完全対称型の2段目はこのような動作になっているので、あえて検討せざるを得ないのである。
結果は右のとおり、左右の2SJ103のgmはその負荷が大きく異なるにもかかわらずほぼ等しい値となっている。これは差動アンプの素晴らしい効果だ。
が、そのgmの値はごく僅かだが異なっている。これは共通ソースが抵抗である場合の限界である。
差動をやめて独立のエミッタ接地動作にしてしまえば、右のグラフに示されるとおりで、条件の違う左右の2SJ103のgmは当然一致しない。これをソースを共通にして抵抗を経由して電源に繋ぐと、すなわち差動動作にすると、上のように左右のgmが一致してしまうという素晴らしい効果が発生する訳だ。
このように、非対称負荷状態にある左右の素子のgmを一致させるという差動アンプの効果は、差動アンプの共通ソース抵抗を定電流回路にして、差動動作の完全性を高めることによってより顕著なものになる。
右のグラフのとおりで左右のgmはピタリと一致する。(高域を除く)
が、差動アンプであっても、負荷の大きい片側に位相補正のためのCを入れた場合の出力電圧及びその位相特性は結局このようになる。
差動アンプであっても、負荷と位相補正Cが非対称であれば、動作の対称性にも限界が生じるのだ。
が、その出力gmの周波数特性と出力電流の位相特性をみると、限界はあっても差動アンプであるからこそこれだけの対称性が維持されているのだ、ということも同時にまた分かるのである。
差動を止めて単独のエミッタ接地動作にしてしまえば当然こうなる。
右側の100pFの位相補正Cによるポールの影響は左側には何の影響も与えない。独立に動作しているのだから当たり前だ。
その出力gmの周波数特性と出力電流の位相特性をみると、差動の場合との差が明白だ。
差動アンプは、本来この状態であるものをあそこまで近い状態に持っていくのである。
この対比を見ると、差動アンプには限界はあるがその効果は大きいということが分かる。
実はこれが、真空管完全対称型DCアンプでは2段目にカレントミラーが使用されるのに、半導体完全対称型DCアンプには2段目にカレントミラーではなく差動アンプが使用される理由なのである。(カレントミラーとは要するに単独動作のエミッタ接地動作)
半導体を終段に起用した場合、それは5極管特性のTRやFETであるためにその電圧ゲインは非常に大きい。このため2段目の右側には左側を遥かに超えた負荷増大効果が生じるのである。結果、2段目素子のCrssやCobあるいはドレイン−ゲート間(コレクタ−ベース間)に入れた位相補正のためのCには巨大なミラー効果も発生する。ところが、2段目の左側にはそのような効果が生じないのである。
すなわち、半導体完全対称型アンプの場合、2段目は終段の上側を担当するか下側を担当するかで天地ほどもの違いがあるのである。
そのような非対称な負荷条件でも2段目が対称な動作をし対称な信号を終段に送り込むためには、そのような条件でも左右のgmが一致し、ポールの影響も対称に近づけることのできる差動アンプでなければならないのだ。
そのような能力のないカレントミラーでは全く役者不足なのである。
では真空管を起用した場合は何故カレントミラーで良いのか? それは終段に起用された真空管が3極管でゲインが小さく、結果終段電圧ゲインが1以下とごく小さいためである。そうであると2段目右側に対する負荷増大効果もほぼないに等しい。だから2段目の負荷条件はほぼ等しいのでカレントミラーでも可能なのだ。
正確に言えば、終段が半導体か真空管かというところではなく、ゲインの大きい5極管特性の素子であるかゲインの小さい3極管特性の素子であるかが2段目の回路構成の違いを生んでいる訳だ。
だから半導体であっても3極管特性の素子、すなわちいにしえのV−FETを終段に起用した場合は、真空管DCパワーアンプと同様に2段目をカレントミラーとしてシンプルに構成した方がスマート。なのかもしれない。今度やってみようかな(^^;
ということが、終段を観ることによってなお一層明らかになるだろう。
そこで、いよいよ終段の2SC959である。
No−168の終段を想定し、エミッタ抵抗47Ωを入れた状態でVbe−Ic特性をシミュレートしてみる。
DCスイープで、V2を0Vから1VまでスイープしIcの変化を電流プローブで直読する。
47Ωの抵抗がエミッタに入ることにより、その電流帰還NFB作用で随分と直線性が良くなっている。
この結果からIc=1mAにセッティングするためにはV2=0.6Vで良いことが分かる。
そこで、次はV2=0.6VdcとしてIc=1mAを流した状態で、今度はV1を0Vから100VまでスイープしてIcの変化を観測し、その結果から2SC960の出力インピーダンスを測定してみよう。
予想ではVceが大きくなるほどにIcの増加度は大きくなるものと思っていたが、結果は逆であった。これを実際に測定しようとするとVceが大きくなるほどにIc増加度も大きくなるのが通例なのだが、あれはすなわち、損失による発熱(ジャンクション温度の上昇)が故のものということになろうか。
Vceが高い方で電流上昇がやや鈍るが、実際の使用状態に近い0Vから60VではVce10Vの上昇でIc0.05mAの上昇と読んで良さそうだ。したがって47Ωのエミッタ抵抗付きのエミッタ接地回路における2SC959の出力インピーダンスは10/0.05=200kΩ(Ic=1mA付近)ということになる。
が、TRの出力インピーダンスはIcが増えると一般に低下する。ので、V2=0.9Vとして、実働状態に近いIc=6mA付近においての出力インピーダンスを測定してみよう。
実働を30V付近として、Vce=0Vから60でのVce60Vの増加でIc0.45mAの増加といったところだろうか。したがってこの場合の出力インピーダンスは60/0.45=133.3であるから、Ro=133.3kΩ(Ic=6mA付近)ということになる。
やはりIc=1mAの場合より低い。が、こうなるのはアーリー効果というそもそものトランジスタの物性によるもので当然のことらしい。
エミッタ抵抗の効果を知るために、エミッタ抵抗がない場合の出力インピーダンスも観測しておく。
先ずは必要なバイアスを知るために、Vce−Ic特性を観測する。
これがトランジスタのVce−Ic特性の指数関数特性であるということになる。
これと比較すると、エミッタに47Ωが入るとあれだけリニアな特性になるということが良くわかる。
ということはともかく、Vbe=0.6VでIc=5〜6mAになるようだ。
Vce60Vの増加でIc5.4mAの増加といったところか。したがって出力インピーダンスは、60/5.4=11.1kΩということになる。
要するに素の2SC959の出力インピーダンスは、Ic=5〜6mA付近ではRo=11.1kΩ程度ということである。これがエミッタに47Ωの抵抗を入れることによって130kΩ程度まで高まるのだ。エミッタに入った抵抗による電流帰還NFBの効果でで入力インピーダンスも出力インピーダンスも高まる。K先生がスーパーサーキット講座で仰っていたとおりの結果なのである。
余談であるが、この出力インピーダンスの測定結果からすると、この2SC959は旧ロットに違いないのではなかろうか。以前の実測からしてそう思えるのだがどうだろう。
すなわち、これは今も世に残っている本物の2SC959(960)より本物の2SC959ということだ。(^^;
さて、2SC959の出力インピーダンスがエミッタ抵抗47Ω時に130kΩ程度ということになると、やはり負荷が最大51kΩとなるNo−168においては、出力インピーダンスと負荷抵抗が無視できるほど離れているとは言えない。だから、終段の電圧ゲインはgm×Rの簡易計算では正確には求められない。gm×(Ro*R)/(Ro+R)により求めなければならない。
そこで、2SC959のgmを測ってみる。入力に1Vacを加え、コレクタに電流をブローブを取り付けると直接gmが計測できる。
ここでは、Ic=6mA程度になるように0.9Vの直流バイアスを掛け、また、No−168の場合を想定してエミッタ抵抗に47Ωを入れてある。
結果は右のとおり。
1Vac入力で19.45mAの電流が出力される。すなわち、gm=19.45mSである。
この際なので、2SC959の素のgmも測ってみよう。それが下。
なを、念のため申し上げれば、現実にこういう回路を組んで同様に測定してみようと思う方がいらっしゃるかもしれませんが、アッという間にトランジスタが昇天する場合もありますので、注意が必要です。貴重な2SC959でそんなことになったら泣けます。(^^;
と、余談はさておき、出力電流256mA、すなわち2SC959のもともとのgmは、gm=256mS。ということだ。これが素子としての2SC959のgmだ。これがエミッタ抵抗が入ったり、コレクタに負荷抵抗が入ったりして回路gmとしてはこれより小さくなる。たとえば上のとおり、エミッタに47Ωが入った場合は19.45mSになる。計算すれば−22.38dBであるから、47Ωのエミッタ抵抗で22.4dBの電流帰還NFBが掛かり、結果として回路gmが19.45mSになった、ということをシミュレーターは教えてくれるのである。もともとの素子ゲインが大きいと同じエミッタ(ソース)抵抗値でもNFB効果は大きくなる。
次に47Ωを元に戻し、今度はコレクタ負荷に1kΩを挿入し、同様に電流ブローブでコレクタ電流を計測する。
これで負荷に1kΩが入った場合の回路gmを測定しよう。
1Vac入力で19.2744mAの電流が出力される。すなわち、gm=19.2744mSである。
1kΩをエミッタ側に移して、同様に電流ブローブでコレクタ電流を計測する。
1Vac入力で19.2744mAの電流が出力される。すなわち、gm=19.2744mSである。全く上の結果と同じだ。
負荷1kΩがエミッタ側に入っていて、その負荷の一方がアースに接地され、さらには2SC959のコレクタがインピーダンス0Ωの電源を経て接地されているので、これはエミッタフォロア(=コレクタ接地)動作であると仰った人もいたようだが、残念ながら外見上はそう見えても、この場合はエミッタ側の1kΩによる電流帰還NFB作用が生じないので、これはエミッタフォロア動作ではなく、全くエミッタ接地動作なのである。
そして、これが完全対称型終段の上側である。勿論、この上↑にあるものが完全対称型終段の下側だ。
この2つを合体すると完全対称型の終段になる。これでNo−168の終段だ。
ただし、上下の2SC956に加える入力信号は逆相でなければPP動作にならない、のでそうしてある。
上下とも出力電流はぴったりと一致している。19.1728mAだ。したがって上下ともgm=19.1728mSである。上側がエミッタフォロア動作である場合は負荷1kΩによる電流帰還NFBが掛かって、そのgmは大幅に小さく表示されないとおかしいのだが、そうならないのは上側もエミッタ接地動作だからである。
ということは今更なのだが、それよりも、上で二つとも単体で動作させた場合、どちらもgm=19.2744mSであった、のに、合体したこちらではgm=19.1728mSと、gmが小さくなってしまっている。
何故だろう。
それは、負荷1kΩに対して上下の2SC959が共に電流を出力するために、結果それぞれからの見かけ上の負荷が等価的に倍の2kΩになってしまうからである。
上下単独ではそれぞれの見かけ上の負荷が倍と重くなったためにgmが僅かに減少する。
が、A級PP動作では上下が協力して負荷に対処するので、アンプ出力点においての出力電流は右のとおり38.3456mA、すなわち回路gm=38.3456mSと大きく上昇している。すなわち、上下単体では19.1728mSだったから、19.1728×2=38.3456とピッタリ倍(+6dB)である。
A級PP動作で終段のゲインが倍になる、というのはこういう訳だ。上下の協力の賜。
負荷を51kΩにしてこの場合の回路gmを測定してみる。
出力電流は11.1941mAである。したがってgm=11.194mSである。
ここで、以上の測定結果を元に計算してみる。
素子固有の相互コンダクタンスをgm、出力インピーダンスをRo、負荷をRとした場合の電圧ゲインAは、
A=gm*(Ro*R)/(Ro+R)
回路gmをGMとすれば、負荷をRとした場合の電圧ゲインAは、
A=GM*R
したがって、
GM*R=gm*(Ro*R)/(Ro+R)
であるから、Roは、
Ro=Gm*R/(gm−GM)
以上の解析から、
負荷0Ω:すなわちエミッタに47Ωが入った場合の2SC959本来のgmは gm=19.45mS
負荷2kΩ:この場合のgm=19.1728mSは回路gmであるから GM=19.1728mS
負荷102kΩ:この場合のgm=11.1941mSも回路gmであるから GM=11.1941mS
これらを代入してRoを求めると、
負荷2kΩの場合 Ro=138.3kΩ
負荷102kΩの場合 Ro=138.3kΩ
と、どちらの場合も2SC959の出力インピーダンスが138.3kΩであると計算される。
上でIc−Vce特性から、エミッタ抵抗47Ωの場合のRo=133.3kΩ(Ic=6mA付近)と求めたが、こちらの計算ではRo=138.3kΩとなった。
誤差の範囲であり、ピッタリだ。と言うべきだろう。
rval=負荷=1kΩ、2kΩ、4kΩ、8kΩ、16kΩ、32kΩ、64kΩのパラメトリック解析で、終段自体の電圧利得とその位相特性を測定する。
結果が右。
負荷1kΩで32dB、負荷64kΩでは62dB強の電圧利得が終段のみで得られことが分かる。一番上でNo−168全体をシミュレートし、そのオープンゲインは低域で44dB、負荷64kΩでは69.5dBであった。No−168の電圧ゲインは殆ど終段で得られているのだ。
さて、本来終段が完全に電流出力であれば理論的にその電圧ゲインは負荷に比例しなければならない。負荷1kΩで電圧ゲイン32dBならば負荷がその64倍の64kΩの場合は電圧ゲインも64倍の68dBにならなければならないのである。が、負荷64kΩでは62dB強だ。
その理由は終段の出力インピーダンスRoが135kΩ程度だからである。
A=GM*(135*100)/(135+100)=GM*100*0.57
と、完全電流出力(Ro=∞)の場合の
A=GM*(∞*100)/(∞+100)=GM*100
の0.57倍≒−5dB≒−6dB弱(^^;となるのもまた理論的な結果だ。
この場合は完全な電圧ドライブであるからCobによるポールは生じないので、このグラフに表れたポールは素子のそもそものft限界によるものである。ゲインによりそのfcが変化するということは、TRの場合、内部疑似CとHie等内部ベース抵抗がポールを形成するということだろうか。
問題は、実際の回路でこのような独立した電圧源(しかも位相が反転した)を上下2SC959のベース−エミッタ間に作れるか。ということである。
真空管時代のOTL・SEPP回路などもこういう回路であったようで、その場合に現実にこのような独立した電圧源信号を上下の真空管G−K間に形成する方法としては、トランスを用いるということであったようである。MJ11月号にちょうどトランスドライブによるSEPPアンプが載っている。
勿論現代K式DCアンプではトランス結合が採用されるはずはなく、直結回路でこれが実現されなければならないのだが、実はこれが比較的簡単に作れることをK先生は示した訳だ。これを実現するのが、下の回路である。
Pチャンネルのある半導体だと比較的簡単にこの電流源の働きをする回路を組めるが、確かにNチャンネルだけしかない真空管では回路が組めないかも知れない。
要するに電流源でベース抵抗1.6kΩをドライブするのである。そうするとベース抵抗が実質的に独立した電圧源として終段2SC959をドライブするのである。「独立」の意味は勿論回路中の他の要素により影響を受けないという意味であり、この場合は負荷R10に発生するアンプの出力電圧でベース抵抗R6に発生する電圧が影響を受けないということである。
何のことはない。終段をドライブする前段が電流出力(=出力インピーダンスが高い)であれば良いのだ。
これにより終段上下は同じくエミッタ接地のPP動作をし、結果右のような電圧利得と位相特性が得られるのである。
負荷1kΩでA=34.5dB=53倍、fc≒350kHz、負荷64ΩでA=62dB=1250倍、fc≒18kHzだろうか。
ただしこの電圧ゲインは正しいかどうかは取りあえず保留だ。何故ならどこが基準電圧になっているか分からないから。
電流源I1の負荷は、その電流ループを考えれば分かるように、単純にR6ではなく、アースとR6間である。要するに下図で電圧差プローブを取り付けた間だ。この間でアンプ出力点からQ2を経由してマイナス電源に分流するループも勿論あるが、それも電源を経由してアースに至るから結局この間にある。したがって、この間の電圧を計測するとそのインピーダンスが計測できる。
そして、そのインピーダンスが電流源I1から見た終段の入力インピーダンスである。
計測結果が右のグラフだ。
負荷1kΩで55.6V、2kΩで106.6V、4kΩで200V、8kΩで358V、16kΩで595V、32kΩで889V、64kΩで1181Vである。電源電圧からしてそんな電圧が出力されるはずは現実にはないのだが、シミュレーターはそういう無意味な制限を口にしない。有意義な理論的数値を示してくれるのだ。
1mAac出力でその出力AC電圧になるのであるから、オームの法則により電圧/電流でそのインピーダンスが計算される。
負荷1kΩで55.6kΩ、2kΩで106.6kΩ、4kΩで200kΩ、8kΩで358kΩ、16kΩで595kΩ、32kΩで889kΩ、64kΩではなんと1.181MΩということである。
これは終段の電流ブースター効果により負荷R10のインピーダンスが終段の電流ゲイン分増大するからだ。インピーダンスの増大が負荷に比例しないで伸び悩むのは、終段自体の出力インピーダンスが上で計測したように135kΩ程度であるため終段のブースター能力が負荷が大きくなるほどに伸び悩むからだ。
が、それにしても終段上側の入力インピーダンスは非常に高いものであることが分かる。
負荷が軽いとか重いとか言う場合、一般的には負荷抵抗値が小さいことを負荷が重いと言う。が、それは電圧出力を暗黙の前提とした話しだ。電圧出力はどのような負荷にも同じ電圧を出力しなければならない。したがって負荷抵抗値が小さいほどに膨大な電流を出力しなければならないから負荷抵抗値が小さいことを負荷が重いという。が、電流出力の場合はこの逆で、負荷抵抗値が大きいほどに負荷が重い。電流出力は負荷抵抗にかかわらず同じ電流を出力しなければならないから、負荷抵抗値が大きいほど通りにくいところに電流を通して高い電圧を出力しなければならない。電流出力の場合は負荷抵抗値が大きいほど負荷が重いのだ。だからこの場合、終段上側は2段目にとって非常に重い負荷なのである。
これに対して電流源I2の負荷はQ2のベース抵抗R7(1.6kΩ)間である。Q2はトランジスタなのでFETや真空管の場合と異なりその入力インピーダンスとエミッタ抵抗R9のシリーズ抵抗値がR7にパラとなったものがI2の負荷になる。この場合もR9は47Ωとして利くのではなくQ2の電流ブースター効果によりその電流ゲイン分増大する。
結果、右の図のようになった。
負荷1kΩ時に1.39V程度、64kΩ時に0.86V程度だろうか。したがって終段下側の入力インピーダンスは1.39kΩ〜0.86kΩに過ぎないのだ。終段上側のおおよそ1000分の1だ。終段下側は電流出力の2段目にとっては上側に比して1000分の1の非常に軽い負荷なのである。だから2段目は終段の上を担当するか下を担当するかで天地ほどの違いがあるのだ。要するに完全対象型の2段目の負荷条件はこれほどまでに非対称になるのである。
さて、この結果で予想外だったのは、終段負荷が大きくなるほどにエミッタ抵抗47Ω込みのQ2の入力インピーダンスが低くなるということだ。
右の結果から、これが負荷1kΩ時10.6kΩ、64kΩ時860Ωと計算されるのだが・・・
ちょっとその理由は浮かんでこない(^^;
が、この結果から終段自体の電圧ゲインと終段に起用したこの2SC959のCobが計算できる。
終段自体の電圧ゲインは、負荷1kΩでは 55.6/1.39=40倍(32dB)であり、負荷64kΩでは 1181/0.86=1373倍(62.75dB)である。これは上で保留した終段自体の電圧ゲインに近い。のは、今回ちょうどR6,R7の1.6kΩの両端電圧が1.0V程度となっているからであろうか。
fcは右の図から負荷1kΩ時で350kHz、負荷64kΩ時で18kHzとみて良いであろうか。
そしてそれぞれドライブインピーダンスと電圧ゲインは1.39kΩ、40倍と0.86kΩ、1373倍であるから、
C=159/(R*fc*(A+1))で2SC959のCobをそれぞれ計算すると、
Cob=159/(1.39*350000*41)=7.97pF
Cob=159/(0.86*18000*1374)=7.48pF
と、読みとり誤差を勘案すれば全く同じと言える結果が得られた。
なんと予想に反してこの2SC969のモデルのCobは7.5pF〜8pFという結果だ。う〜ん、Vceが27Vとある程度高いことはあるが、こんなに良い数値でよいのだろうか。(^^;
このモデルでシミュレートしたNo−168の高域特性がK先生実測のオリジナルNo−168より良いのは、このモデルのCobがこのように小さく、K先生が使用された実際の2SC959L08BのCobはこれより大きいせい・・・、と言えるかもしれない。だって、ここで使っている2SC959のモデルは同じ2SC959でも旧ロットだから・・・ って、ほんと(^^;
2段目と終段を接続する。
これまでの解析で、2段目2SJ103の出力インピーダンスは3MΩであり、その負荷となる終段の入力インピーダンスは終段上側が55.6kΩ(負荷1kΩ時)〜1.181MΩ(負荷64kΩ時)、下側が1.39kΩ(負荷1kΩ時)〜0.86kΩ(負荷64kΩ時)であることが分かっている。
この条件は上で2段目差動アンプの負荷を左右で違えてシミュレーションした条件より遥かに左右の負荷条件の乖離が著しい。
このように天と地ほども負荷条件が違う2段目ははたして対称動作が可能なのであろうか。が、テーマ。
2段目差動アンプの左右ドレインの出力電流を見ることによってそれは明らかになる。
先ずは負荷が1kΩの場合だが、この場合の負荷条件=終段入力インピーダンスの違いは55.6kΩと1.39kΩである。
低域で1.9mA、すなわち左右ともそのgm=1.9mS程度であるが、多少の差が生じていることが分かる。
さらに、右側のgmは500kHz付近で低域の1/1.41421536倍、すなわち−3dBとなっている。
これは2SJ103のCiss=18pFとCrss=3.6pFが1.8kΩとで作るポールによるものだ。
また、この場合、左側のgmは単独ではそのような低い位置にポールはないので同様に30kHz付近から低下することはあり得ないのだが、差動アンプの効果で差動の右側に追随しているのである。
が、追随しきれていないのは差動アンプの限界だ。
折角なので、2段目が差動でない場合はどうなるか見てみよう。
これで2段目差動アンプのありがたみが分かる。し、2段目が単なるカレントミラーでは駄目なことも分かる。
当たり前だが差動アンプのような相互作用がないので、2段目出力のgmの乖離が大きく、また、ポールも左右でバラバラである。
次は負荷が64kΩの場合だが、この場合の負荷条件=終段入力インピーダンスの違いは1.181MΩと860Ωというとてつもないものになる。1373倍もの違いだ。
う〜む。
さすがにかなり対称性は破れてきた。
これは、1つには終段上下の入力インピーダンスが1000倍以上も違うことによるものであり、今ひとつは結果2段目右側のドレインベース間が左側のそれの1000倍以上の電圧振幅で振られるためにCrssに働くミラー効果に1000倍以上の差が生じるためである。
差動アンプはこれを右のレベルまで押さえているのだが、やはり限界があるわけだ。
こうしてみると終段の電圧ゲインが非常に大きいので、2段目上側2SJ103の入り口には1.8kΩとミラー効果で巨大に拡大されたそのCrssによるポールが22kHz付近に出来ている。
最終的には、それが終段のポールと連星効果で合体して1つのポールになっているわけだ。
もはや見るまでもないと思うが、2段目が独立のエミッタ接地の場合。
こうも乖離してしまってはどうにもならないだろう。
終段の電圧ゲインが大きい半導体完全対称型では、2段目が差動アンプであることが必要なのだ。
カレントミラーでは駄目なのである。
差動アンプ型式に戻り、差動動作の完全性を高める努力でどこまで2段目の動作対称性を高められるかを考える。
まず、初段差動アンプを解析した際に不平衡対称動作でもその対称性を飛躍的に高めた共通ソース抵抗の定電流回路化である。
ここでは理想的な定電流回路である電流源に置き換えてみる。
やはり定電流回路は非対称な負荷により乖離が必然な左右の素子のgmを強力に一致させる効果が絶大なのだ。
多分これこそ差動アンプが本来叶える機能なのだろう。定電流回路はそれを理想的にするのだ。
また、非対称な位相補正Cによる左右の乖離も少なくなっている。
が、残念なことに十分ではない。
定電流回路をもとの抵抗に戻し差動アンプの右側にカスコード回路を入れてみる。
う〜ん、素晴らしい。
これほどまで対称性が高まる。
終段上側を担当する差動アンプの右側にカスコード回路を入れることの意味はこれほど大きいのだ。
2段目差動アンプに付加するカスコード回路は耐圧不足だからではなく、2段目差動アンプの対称性をより理想的にするためなのだ。
が、子細に見れば、カスコード回路自体には左右のgmを強制的に一致させる定電流回路のような能力はないことが分かる。
グラフを見れば分かるように低域でもgmは完全には一致していない。
すなわちここで左右のgmが近づいたのは単にカスコードアンプが2段目右側への終段の負荷効果を遮断したことによる結果的効果なのだ。
その意味では高域での乖離の縮小も、同じくカスコード回路が終段の負荷効果を遮断しミラー効果を遮断した結果的効果と言えるかもしれない。
では、定電流回路とカスコード回路を併用してはどうか。
素晴らしい!
超高域を除き実に理想的な対称性を備える状態になった。
ここまでやれば完璧だろうか。
完全対称型旧世代のように2段目差動アンプの右側にCを挿入して位相補正する場合でも、カスコード回路を入れた方が良いことが右で分かる。
2SJ103のCrssより大きい5pFを挿入してシミュレートしてみる。
結果を上の共通ソース抵抗が3kΩのカスコードなしの場合と比較してみると分かる。
乖離はこの程度だ。
これに、定電流回路のgm強制一致能力を加えればどうだろうか。
高域を除けば実に理想的な対称性を備えた状態になった。
2段目差動アンプの右側例の位置のCで位相補正したK式旧世代の完全対称型でも、差動アンプさえ理想的な動作条件を備えてやれば、これだけ対称な動作が可能なのだ。
以上、終段のゲインが大きい半導体完全対称型では、真空管式のそれと違って、2段目が差動形式であることが必要だということが明らかだろう。
この辺、某編集部の皆様にもご理解を賜ると幸いなのだが・・・(^^;
さて、ようやく最初に戻ってこれまでの各部を組み立ててNo−168の全体回路を組む。
初段の位相補正だけを外して各部の電流出力を電流プローブで観測する。アンプ出力の負荷は1kΩである。ボリュームMINの状態だ。
アンプ入力に1Vacを加えているので各部の電流出力値は換算の必要もなくそのままmAをmSに置き換えてgm値とすれば良いのである。
一番下が初段の電流出力であるが0.835mAである。したがって初段のgm=0.835mSである。上で初段を解析した時と同じだ。
下から2番目が2段目差動アンプ出力点での電流出力で2.895mAである。したがって2段目出力までのgm=2.895mSである。であるから2段目自体のgmは2.895/(1.8*0.835)=1.938mSである。上で2段目を解析した際もその程度だった。
終段出力での電流出力は77.3mAであるからその点までのgm=77.3mSである。上での解析でアンプ負荷1kΩの場合の終段の入力インピーダンスは1.39kΩであったから、終段自体のgmは77.3/(1.39*2.895)=19.21mSということになる。上で終段のみを解析した際の負荷1kΩPP動作時のC959の回路gm=19.1728mSであったから誤差の範囲でありピッタリである。
結果、アンプ出力端では終段PP動作によるgmが6dB=2倍にアップして156.7mA、すなわちgm=156.7mSとなっている。
結果負荷1kΩの場合の電圧ゲインは156.7mS×1kΩ=156.7倍=43.9dBとなるわけだ。
そのゲイン配分は、概略初段=1.5倍、2段目2.7倍、終段38.4倍である。
余計なことを言えば、これは最近の完全対称型パワーアンプにおける思想には合致していない。プリのフラットアンプのゲインは殆ど終段が稼いでいるのである。信号源に近いところでゲインを稼ぎ、高い信号レベルでその伝達をすることが良い音をもたらす、ということであれば、いずれ半導体プリのCDラインアンプ(フラットアンプ)にもゲイン配分の変更などの改変の時期が来るかもしれない。
2段目電流出力のグラフが100kHzを超えたところから非対称になるのは、これまでの解析から2段目右側にのみこの位置で発生するポールの影響を差動アンプが完全には左右対称に制御出来ないことによるものだ。
終段出力点における電流出力のグラフも同様に100kHzを超えたところから非対称になるが、これは2段目の非対称を受け継いだ結果だ。
が、最終的にアンプ出力点においてはそれを引きずっていないのが幸いだ。
また、このアンプの第1ポールは、基本的に終段入り口の1.6KとC959入力インピーダンスの並列合成抵抗とC959のCobが終段電圧ゲインによるミラー効果で拡大した容量で終段入り口に発生するポールであることも明らかだ。
ただし、2段目右側の2SJ103のCrssが終段の電圧ゲインによるミラー効果で拡大された容量と初段負荷抵抗で2段目入り口にも近い位置にポールが発生している。
が、これらは連星効果により解け合ってしまい、結局終段入り口に低いポールがひとつあるという状況になる。それが1番上でみたfc≒90kHzのポールだ。
次にアンプの負荷が64kΩの場合である。No−168のボリュームは50kΩなのでボリュームMAX時で最大負荷は51kΩだが、まぁいいでしょ。(^^;
この場合も初段のgmは負荷1kΩの場合と同じでgm=0.835mSである。
2段目出力のgmは少し小さくなって2.4mSである。したがって2段目自体のgm=2.4/(0.835×1.8)=1.6mSである。これも上で2段目を解析した時にその程度だったはずだ。
2段目にカスコードがないために僅かに右側のgmが小さいとともに、右側2SJ103のCrssによるポールの影響を完全には押さえられないための乖離が3kHz以上の高域で生じている。
終段出力のgmは22.5mSと負荷1kΩ時の1/3となってしまった。終段自体のgmは上での解析でアンプ負荷64kΩの場合の終段の入力インピーダンスが0.86kΩであったから、22.5/(0.86*2.4)=10.9mSである。上で終段の解析をしたときにはこの場合の終段自体のgm=11.1941mSであった。誤差の範囲だろう。
結果アンプ出力端では6dBアップして、すなわち倍になってgm=45mSとなっている。負荷1kΩの場合に156.7mSであったから28.7%になってしまった訳だ。−10.8dBである。
この理由は2段目差動アンプの出力インピーダンスと終段の出力インピーダンスにある。ということはこれまでの解析でみたとおりだ。
以下、2段目の動作対称性を高める手だてを講じて、その効果を観る。
先ずは共通ソース抵抗の定電流回路化。
以下、グラフ上がアンプ負荷1kΩの場合で、グラフ下が負荷64kΩの場合だ。
負荷64kΩの場合で明らかなのだが、やはり2段目のgmがピッタリと一致している。
が、2段目Crssによるポールの非対称の抑圧は定電流回路化しても改善効果は小さい。
それともう一つ。負荷64kΩの場合で顕著だが、何故か終段上下のgmにかえって乖離が生じてしまっている。何故だろう?
次は、2段目にカスコード回路を付加した場合。
別に回路の図形的対称性で「対称や否や」を論じるセンスはないし、もとより図形的対称性を追う必要もないので、動作対称性向上のために本質的に必要な右側だけにカスコード回路を付加する。
ここにカスコード回路を付加することが、動作対称性を向上させる上で非常に効果的であることが明らかに分かる結果だ。
2段目差動アンプのgmは低域だけでなく、高域まで非常に良く一致する。これは、2段目右側差動アンプの負荷が入力インピーダンスの低いゲート接地2SJ103のソースとなって、左右の差動アンプの負荷条件が近づいたこと、と、同じくカスコードアンプによって2段目右側に生じるミラー効果が排除されて、ポールの非対称な発生がなくなったことによるものである。
定電流回路のように左右の差動アンプの動作対称性を強制的に揃えるような効果ではないが、カスコード回路は完全対称型の対称性の破れを生じる根本原因を見据えた優れた対処法であることが分かるだろう。
が、この場合も負荷64kΩ時に終段上下のgmに明確な乖離が生じている。何故だろう?
次は、定電流回路とカスコード回路の併用で最善の結果を期待するもの。
やはり、最良の素晴らしい結果になった。(^^)
と言いたいところだったのだが、他はまさにそうなのに、負荷64kΩ時にこれまで以上に明確に終段上下のgmの乖離が発生している。
何かおかしい。
もしや、2段目カスコードを右側だけに入れたことがまずかったのかもしれない。ので両側に入れてやってみる。
やはり同じだ。負荷64kΩでは終段上下のgmに乖離が生じる。何故だ?
さらに、定電流回路を加えてみる。
やはり終段上下TRのgmに乖離が生じる。
なにか2段目の動作対称性を揃えた方が終段上下のgmの乖離が大きくなるようにも感じられるではないか。
分かった。
それは、完全対称型に必然となる終段上下のTRのアイドリング電流の僅かな乖離によるものなのだ。
終段下側の2SC959には、2段目差動アンプ右側のアイドリング電流というか動作電流(No−168では0.5mA〜0.6mA程度)分、終段上側より大きいアイドリング電流が流れるのである。要するに終段下側は2段目差動アンプ右側に流れる電流の流路なので、終段下側のアイドリング電流は終段上側に流れるアイドリング電流+差動アンプ右側の動作電流になるのである。このようにして2段目右側の電流流路を確保しなければ当然出力にDCオフセットが生じてしまう。そのために完全対称型は、その分終段下側に上側より多くの電流が流れるように初段差動アンプのトリマー調整等で微妙に対称性を崩してオフセットを解消しているのである。
No−168では終段上下のアイドリング電流の差は勿論2段目差動アンプ片側の動作電流である0.5mA〜0.6mA程度とほんの微量である。が、終段のアイドリング電流設定が5mA〜7mAであることからすればその1割だ。とても微量とはいえないという見方もあろう。
そして、このアイドリング電流の1割の差が終段上下のgmにこれだけの乖離を生じさせるのだ。
これまでのシミュレーション結果からすると、終段のこの乖離は2段目出力までの対称性を高めることでより鮮明になる、と言えるのかも知れない。
と、確信を持って言うのは、この問題への対応策を講じることにより終段上下のgmの乖離が解消されるからである。
そして、その対応策の一例がこの回路である。
かつてNifのAVフォーラムで提案された方法で、要するに2段目差動アンプ右側の動作電流を定電流回路で−電源に抜き取り、終段上下のアイドリング電流を一致させて、終段動作の完全対称性を高めるという手法だ。
負荷64kΩの場合だが、終段上下のgmもピッタリ揃っている。
2段目差動アンプのgmもピッタリである。これなら2段目差動アンプの共通ソース抵抗を定電流回路にする必要もなさそうだ。
とは言っても一応3kΩを定電流回路にした場合も観ておく。
終段高域におけるgmの乖離も改善されている。
その意味ではあった方がより理想的ではある。
と、つれづれなるままにNo−168のシミュレーションをやってきた。が、ちょっと長くなりすぎた。(^^;
まだまだ十分ではないようにも思えるが、一応この辺で打ち止めにしよう。
で、最後に毎度のことだが、以上のシミュレーション結果及び拙い解析、もちろんな〜んの保証もない。ので、悪しからず。
2003年10月18日
(正しいシミュレーター活用の基礎知識その1)
「1Vacを入力して出力AC電流を直読すればそれがgmを表すことは分かるが、現実この回路で動作するかね(−−)。入力で飽和するだろ!」と、鋭いご指摘を頂いてしまった。
お〜!!、言われてみればそのとおり。これはまたド素人ぶりを晒してしまったわな〜(^^;
「そういうときには、例えば10mVacのような現実的な入力を加えて、電流プローブの測定値を表示するのではなく、「Ic(Q1)/V(V3:+)」というgmを求める計算式の結果を表示させれば良いのだよ。」
と、ありがたくも正しいシミュレーター活用の基礎知識も御教授頂いた。m(__)m
ので、早速正しい手法によるシミュレーションをやってみた。
結果は・・・
同じだった〜、安堵(^^)
上はとりあえずシミュレーターが制限項目とせず理論値を表示してくれる範疇の非現実的設定ということですんだようだ。ので、取りあえずは上のシミュレーション結果についての大規模改訂は保留。ということで(^^;
2003年10月23日